электромагнитная теория гравитации

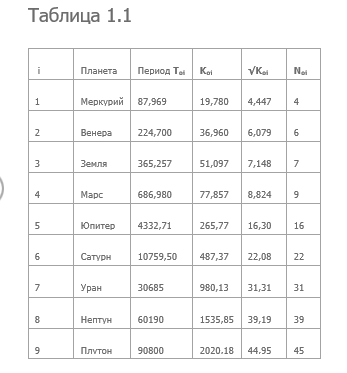
Электромагнитная теория гравитации

ЭМТГ стартует из одного из фундаментальных законов сохранения. В итоге, не выходя за рамки классической физики, выводится волновое уравнение. В полученном волновом уравнении, в отличие от общепринятых волновых уравнений, применяемых в современной физике, присутствует некая функция, которая объясняет смысл квантовой механики, принцип неопределенности Гейзенберга и т.д., возвращая многие физические проблемы в лоно классической физике. Кроме того, было получено, что эффект притяжения периферийного тела к центральному формируют силы электромагнитной природы с конкретным видом электрической и магнитной составляющих. Также из анализа полученных результатов следует, что электромагнитное поле является переменным, причем электрическая и магнитная составляющие центрального тела колеблются по определенным законам, которые можно графически визуализировать. В качестве доказательства вышеизложенного приведем несколько примеров.

1. Построение графика для планет Солнечной системы с ярко выраженными квантово-механическими атрибутами.

Третий закон Кеплера гласит: квадраты периодов обращения планет вокруг центрального тела пропорциональны кубам больших полуосей их орбит:

Т²=4π²а³(GM)      (1.1.2)

Представим (1.1.2) в виде:

а = (GM/4π²)^1/3(Т²)^1/3

где: G - постоянная гравитации М - масса центрального тела

Теперь произведем обозначения:

λ_i=(GM/4pi;²)^1/3 = const      (1.1.4)

K_ij = (T²_ij)^1/3      (1.1.5)

i - индекс планетной системы

j- индекс планеты (спутника)

λ_i - константа для i-ой планетной системы.

Тогда (1.1.3) можно переписать в виде:

а_ij=λ_iK_ij      (1.1.6)

Формула (1.1.2) достаточно хорошо согласуется с астрономическими наблюдениями. По формуле (1.1.4) для Солнечной системы вычислим значение λ₀ в единицах суток и миллионов километров: λ₀ =2.933 млн. км/ (сут)^2/3

и для простоты опустим в дальнейшем размерность λ₀ и К_0j (будем считать их безразмерными). По формуле (1.1.5) рассчитаем К_0j и K_0j^1/2 для всех планет Солнечной системы (Таблица 1.1.1). Кроме того, введем целые числа N_0j, равные приближенным до целого числа значениям.

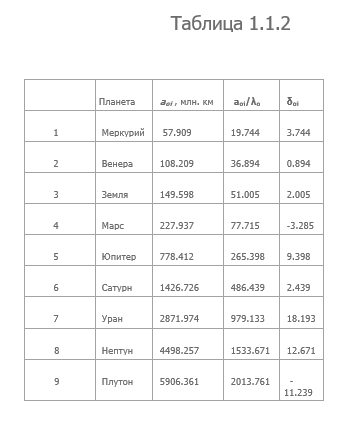
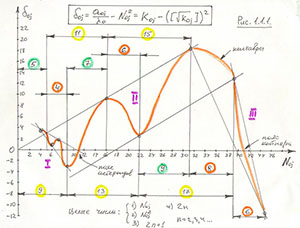
Числа N_0j мы вводим для того, чтобы произвести анализ третьего закона Кеплера на возможность зависимости орбит планет от каких-либо целочисленных комбинаций. Как известно, в 1885 году И. Бальмер установил, что длины волн известных в то время линий спектра водорода зависят от квадрата целых чисел, что и сыграло в дальнейшем большую роль в создании теории атома. Поэтому, если мы обнаружим какую-либо целочисленную зависимость, то это нам подскажет, каким образом строить теорию гравитации.

Введем величину δ_0j = (а_0j/λ₀) - N_0j² и, на основании результатов Таблицы 1.1.2, построим график зависимости δ_oj= f(N_0j), изображенный на Рис.1.1.1 (масштаб ∆δ_oj равен масштабу ∆N_oj).

В результате, получается график:

Видео данного алгоритма:

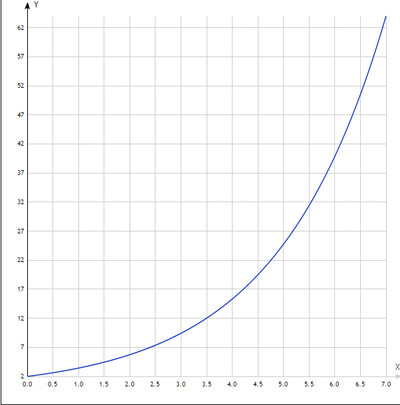
Получен очень важный результат в том плане, что он подрывает мистификацию микромира с его квантово-механическим способом описания. Квантовая механика "проникла" и в макро-мир. Она, наряду с ньютоновской механикой, описывает параметры орбит планет Солнечной системы. Это значит, что и в микро-мире, равно, как и в макро-мире, где теперь, наряду с механикой Ньютона, работает и квантовая механика, должна также работать и ньютоновская механика. Обе механики - и квантовая, и ньютоновская - дополняют друг друга, но никак не противопоставляются.

1. По ходу решения задачи аналитическим образом была получена формула, применение которой универсально во многих астрономических расчетах (формула приведена в приближенном виде):

R = R₀{(√5 +1)/2}ⁿR₀(1,6)ⁿ

где: n =0,1,2,3… - целочисленный показатель степени.

(√5 +1)/2 = 1,61803398875....≈ 1.618 - так называемое "золотое сечение"

R₀ - начальный параметр

Рассмотрим некоторые примеры ее применения.

При R₀, равному радиусу Земли, при различных значениях n имеем границы радиационных поясов Земли и зону расположения Луны, прекрасно согласующиеся с табличными данными.

При R₀, равному радиусу Меркурия (R₀=2,4 тыс. км), получаем радиусы планет Солнечной системы:                                                      

 

1) n=0           R равен радиусу Меркурия 2,4 тыс. км                            

2) n=1           R=3.9 тыс. км.

  

 Радиус Марса (табличное значение) равен 3,4 тыс. км.

 

        3) n=2           R=6.2 тыс. км.

 

 Радиус Венеры равен 6,1 тыс. км.

 

 Радиус Земли равен 6,4 тыс. км

 

         4) n=5           R=25,6 тыс. км

 

  Радиус Нептуна равен 24,8 тыс. км.

 

  Радиус Урана равен 26,2 тыс. км.

 

         5) n=7           R=65,5 тыс. км

 

     Радиус Сатурна равен 60,3 тыс. км

 

     Радиус Юпитера равен 71,4 тыс. км.

  

Сравнивая полученные результаты с табличными данными, видна определенная корреляция истинных величин вокруг рассчитанных. Например, радиусы Венеры и Земли расположены вокруг рассчитанного значения (при n=2) следующим образом: 6,1 тыс. км (Венера) – 6,2 тыс. км (рассчет) -6,4 тыс. км (Земля).







Объяснение этого факта выходит за рамки настоящей работы.

 

  

2.3 Как продолжение пункта 2.2,  рассчитаем радиусы орбит спутников Марса: Фобоса и Деймоса. В пункте 2.2 мы получили значение радиуса R=3.9 тыс. км. Используя данное значение как радиус Марса R0,  получаем при n=2 и n=4 соответственно: 

    - радиус орбиты Фобоса 10,0 тыс. км. 

    - радиус орбиты Деймоса 25,6 тыс. км

  

Табличные данные орбит этих спутников таковы: 

    - радиус орбиты Фобоса 9,4 тыс. км. 

    - радиус орбиты Деймоса 23,5 тыс. км.

  

Теперь в формулу подставим табличное значение радиуса Марса R0=3,4 тыс. км. Соответственно, при n=2 и n=4 получаем: 

    - радиус орбиты Фобоса 8,7 тыс. км. 

    - радиус орбиты Деймоса 22,3 тыс. км.

  

Сравнивая табличные данные с полученными при разных значениях радиуса Марса, мы видим, что табличные данные находятся «посередине» между расчетными величинами. Так же, как и в пункте 2.2, объяснение этого факта выходит за рамки настоящей работы, так как смысл подобных демонстраций – только лишь в показе зависимости параметров небесных тел от целочисленных значений переменной n  в формуле. Коротко лишь отметим, что в пункте 2.2 рассматривается система, центральным телом которым является Солнце, принадлежащее одному энергетическому масштабу, а в пункте 2.3. – другая система, где Марс принадлежит другому энергетическому масштабу.

  

 

2.4. При R0, равному радиусам планет – гигантов, и при n=1 по формуле получаем границы расположения их  колец.

  

2.5. По этой же формуле рассчитываются радиусы орбит планет Солнечной системы.

  

 Таким образом, приведенных примеров достаточно для того, чтобы любой человек, не имеющий специального образования, мог удостовериться в том, что целые числа (в частности, показатель степени n в вышеупомянутой формуле, числа К, N и комбинации 2n и 2n+1 на графике) свидетельствуют о квантово-механическом способе описания данного явления.



Данное исследование параметров планет Солнечной системы явилось стартовым для создания электромагнитной, или, в общем случае, полевой теории гравитации. Соответственно, открылся новый путь к пониманию

метафизики абсолютных понятий.