23:20:50 Структура поля | |
В полевой теории гравитации получена формула с золотым сечениемПо ней рассчитывается основная линейка силовых линий поля двухкомпонентного вихря. Это видно на примере с семейством эллипсов магнитной компоненты поля. Например, произвольным образом среди бесконечного количества эллипсов семейства зафиксируем симметричную пару эллипсов и обозначим их №1.  Пусть эти эллипсы имеют конкретные параметры (большая, малая полуоси и др.). Исходя из параметров зафиксированной пары эллипсов, параметры соседних эллипсов будут определяться из них при помощи формулы с золотым сечением. И опять, как в публикации Структура поля в пространстве между силовыми линиями, зададимся вопросом: а какова структура поля между силовыми линиями? Ранее было сказано, что структура ламинарная. Но что это значит и какая именно "ламинарная структура"? На этот вопрос отвечает закон Бальмера-Ридберга: поле между двумя силовыми линиями, определяемыми при помощи формулы с золотым сечением, имеет вторичное квантование. И это квантование описывается общеизвестной формулой данного закона. То есть, если формула с золотым сечением описывает закономерности поля в целом на пространстве от нуля до бесконечности, то закон Бальмера-Ридберга описывает поле уже в конкретной и конечной области, ограниченной с обеих сторон. Называя вещи своими именами, можно сказать так: формула с золотым сечением описывает стабильные параметры поля, а закон Бальмера-Ридберга - метастабильные между соседними стабильными. "Стабильные" по той причине, что это целый комплекс параметров, в том числе и конструкционные. "Метастабильные" по той причине, что они появляются как следствие из основных параметров. Мало того, квантование силовых линий по закону Бальмера-Ридберга осуществляется все дальше и дальше вглубь в пространстве между силовыми линиями: вначале между стабильными силовыми линиями (семейство эллипсов, изображенное синим цветом): 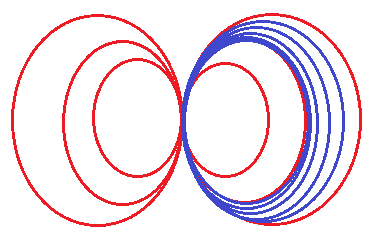 затем между метастабильными силовыми линиями (семейство эллипсов, изображенное зеленым цветом): 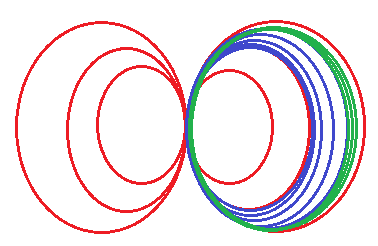 и так далее. Таким образом, осуществляется дискретно-непрерывное ламинарное заполнение полем всего пространства. Учитывая трехмерность вихря, силовые линии переходят в силовые поверхности. В частности, для магнитной компоненты (семейство эллипсов) - это торы. Однако, глядя на последний рисунок, видно, что концентрация метастабильных силовых линий в области стабильной силовой линии - не симметричная: со стороны центра симметрии семейства ( со стороны точки сопряжения эллипсов) наблюдается разрежение метастабильных линий при подходе к стабильной, а с другой стороны стабильной линии - концентрация, точнее схождение метастабильных линий к стабильной силовой линии. Та же картина наблюдается и при квантовании линий между двумя метастабильными линиями. Это, в своем роде, напоминает сжатую пружину с неоднородным коэффициентом сжатия. | |
|
| |
Метафизика – то, что над физикой
Словарь СЗЕФ: метафизика – это философское учение о граничных внеопытных принципах и началах бытия, знания и культуры
Джон Форбс Нэш-младший: Я верил в числа и термины, уравнения и логику, в здравый смысл... Но, проведя жизнь в подобных изысканиях, я не знаю, что такое логика, что определяет здравый смысл... Я прошел долгий путь через физику, метафизику, иллюзию... и обратно. И я сделал самое важное из своих открытий. Главное открытие моей жизни - логичные основания можно выявить только в таинственных уравнениях любви.
Перезагрузка
