12:52:40 Формула Бальмера-Ридберга | |
Формула закона Бальмера-Ридберга для водородоподобных атомоввыглядит следующим образом:  где: λ — длина волны света в вакууме; R — постоянная Ридберга для рассматриваемого химического элемента; Z — атомный номер, или число протонов в ядре атома данного элемента; n1 и n2 — целые числа, такие, что n1 < n2. Данная формула описывает один из фундаментальных законов физики. Зададимся вопросом: насколько информативна она? Первым делом, уточним, что формула имеет зависимость от двух переменных n1 и n2 во второй степени таким образом, что переменная n1 является переменно-фиксированной: при расчете длин волн определенной серии, n1 принимает конкретное значение и первый член в скобках превращается в константу. Следовательно, формулу Бальмера-Ридберга для определенной серии можно переписать в виде: 1/λ = RZ2(const-1/n22) В общем виде получаем: 1/λ = CONST-RZ2/n22 где CONST=RZ2const Произведем еще одно преобразование: CONST-1/λ=RZ2/n22 и обозначим: Y1=CONST-1/λ Y2=RZ2/n22 причем Y1=Y2. Таким образом, путем нехитрых преобразований мы привели формулу Бальмера-Ридберга к виду, удобному для анализа. Первым делом рассмотрим функцию Y2=RZ2/n22 Она имеет вид (Формула Бальмера-Ридберга и ЭМТГ: постановка задачи): YN=А(N)/x2 где А(N)=RZ2 x2=n22 Проверим, выполняется ли для нее условие размерности. Как известно, производная функции dY/dx - величина безразмерная. Поскольку переменная n2 имеет размерность числа, то такая же размерность должна быть и у Y2. Мало того, это доказывается математически. Для этого нарисуем семейство кривых YN=А(N)/x2 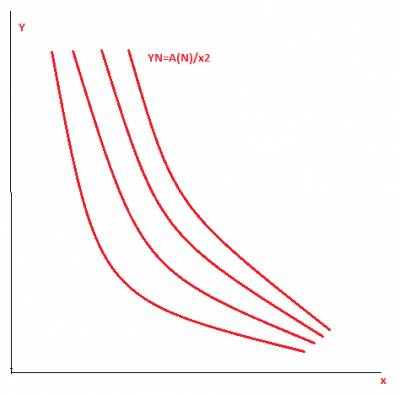 Теперь проведем прямые АВ и АС таким образом, как показано на рисунке: 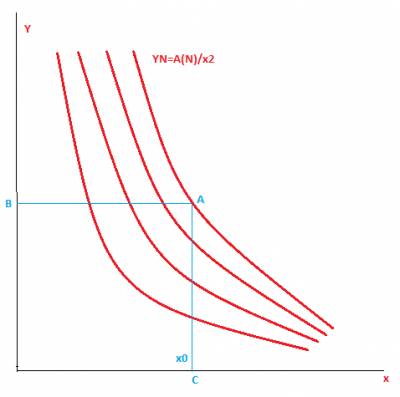 АС пересечет ось Х в точке х0 Через точки пересечения АВ и АС с кривыми семейства проведем прямые: 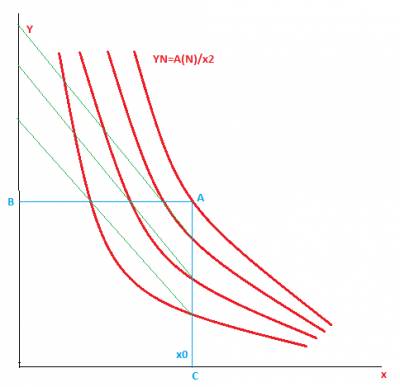 В ЭМТГ доказывается, что, при определенных условиях, эти прямые пересекутся в единственной точке, лежащей на оси Y. И координаты этой точки будут следующими: х=0 y=2х0 Это позволяет осуществить масштабирование осей X и Y в единых единицах измерения, что чрезвычайно важно для всестороннего анализа параметров семейства. Следует лишь дополнить, что, как следует из анализа, проводимого в ЭМТГ, в определении размерности функции Y(x) участвует также постоянный параметр, содержащийся в числителе формулы, однако это невозможно произвести в формуле Бальмера-Ридберга, поскольку постоянная Ридберга R является конгломератом физических констант, а с Z это делать не возможно в принципе. Если для соблюдения размерности функции Y(x) специально ввести некий коэффициент размерности, то действовать он должен опять же на коэффициент Ридберга, который, как уже отмечалось выше, составлен из физических констант. Перенос R в Y1(x) также не приведет к необходимому условию, так как должен присутствовать член А(N). Теперь обратимся к функции Y1=CONST-1/λ Из нее явным образом видна размерность длины в минус первой степени. Поскольку Y1=Y2 то и размерность функции Y2 также равна размерности длины в минус первой степени. Эту размерность вносит константа, входящая в уравнение. Таким образом, можно сделать вывод, что формула фундаментального физического закона Бальмера-Ридберга имеет многопараметрический вид, который требует детального исследования. | |
|
| |
Метафизика – то, что над физикой
Словарь СЗЕФ: метафизика – это философское учение о граничных внеопытных принципах и началах бытия, знания и культуры
Джон Форбс Нэш-младший: Я верил в числа и термины, уравнения и логику, в здравый смысл... Но, проведя жизнь в подобных изысканиях, я не знаю, что такое логика, что определяет здравый смысл... Я прошел долгий путь через физику, метафизику, иллюзию... и обратно. И я сделал самое важное из своих открытий. Главное открытие моей жизни - логичные основания можно выявить только в таинственных уравнениях любви.
Перезагрузка
