В четвертом веке до нашей эры древнегреческий философ и математик Евдокс Книдский, ученик Платона, создал общую теорию отношений. Она была опубликована в 5 книге "Начал" Евклида. Формула этой теории a/b=c/d почти две тысячи лет была практически единственной формулой в физике. Архимед в третьем веке до нашей эры создал свою теорию рычага на основе общей теории Евдокса. Его же способ определения поддельного золота также основан на теории отношений (легенда о голом Архимеде, с криком "Эврика!" выбежавшем из бани). Также в третьем веке до нашей эры Эратосфен Киренский, благодаря теории Евдокса, с большой точностью вычислил радиус Земли, измеряя глубину проникновения солнечных лучей в колодцы в полдень в разных городах Египта (Александрия и Асуан), о чем засвидетельствовано в трактате Клеомеда «О круговращении небесного свода». Со временем в формуле отношений появились комбинации величин, величины в разных степенях и др. Подтверждением тому является третий закон Кеплера, как отношение больших полуосей эллиптических орбит планет Солнечной системы в третьей степени к периодам обращения планет во второй степени. Общая теория отношений Евдокса Книдского и ныне является одной из базовых теорий не только математики, но и всех точных наук.
В 18 веке Эйлер совершил физико-математическую революцию, разорвав формулу Евдокса a/b=c/d на две части и в промежутке между частями введя новую физическую величину скорость V.
В своей книге “Механика или наука о движении, изложенная аналитическим способом”, опубликованной в Петербурге в 1736 году, Эйлер пишет:
О всяком теле, которое движется, говорят, что оно имеет быстроту или скорость, и эта скорость измеряется тем расстоянием, которое тело, двигаясь равномерно, проходит в данное время.
Значит скорость тела, движущегося равномерно, может быть абсолютно измерена тем расстоянием, которое в данный промежуток времени, скажем в секунду, проходит тело. И нужно считать, что тот, кто может определить расстояние, которое в секунду проходит какое-либо тело, может вполне знать скорость этого тела.
За единицу скорости Эйлер предлагал брать рейнские футы за секунду времени (1 рейнский фут = 0,31385 метрам).
Математики и физики поняли, что способ Эйлера открывает им широкие возможности в науке. Ведь до этого практически не было формул. Даже законы Ньютона, закон Всемирного тяготения и мн.др. описывались словами. Открытие новых величин в газодинамике, электромагнетизме, гидродинамике, оптике и др. требовало обоснования их связи с базовыми величинами. Для этого исследователям необходим был аналитический "язык", описывающий законы и закономерности в лаконичной символьной форме. Благодаря открытому Эйлером способу формулопостроения, в девятнадцатом веке начался расцвет точных наук.
Но вернемся открытию Эйлера: первая формула, полученная путем разрыва формулы Евдокса, была скорость V:
a/b=V=c/d
Эйлер, собственно, это сделал для математики. Зададимся вопросом: зачем Эйлеру понадобилась скорость?
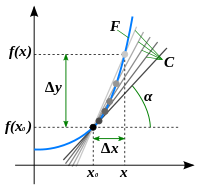
Эйлер исходил из того, что V=Δx/Δy - это прямая линия между точками с координатами (х1, у1) и (х2, у2), лежащими на кривой вида f. Чем меньше отрезки между точками, тем точнее линии V отражает контуры функции f (с "квадратурой круга" до Эйлера работали многие математики, в том числе пифагорейцы, Евклид, Ньютон и мн.др., описывая окружности при помощи вписанных многоугольников и т.д.). При dх и dу, стремящимися к нулю, линия V касается функции f только в одной единственной точке.
И тут Эйлер понял смысл производной к функции f : линия V - это мгновенная скорость изменения функции.
Таким образом, производная - это мгновенная скорость (в точке, а не на отрезке!!!) изменения функции. Если функция линейная (нет ускорения), то мгновенная скорость одна и та же во всех точках функции.
Первым обозначать приращения аргумента и функции греческой буквой Δ (дельта) начал швейцарский математик и механик Иоганн Бернулли (1667 — 1748). Немецкий математик Г.В. Лейбниц (1646 — 1716) ввел дифференциалы dx и dy. Способ обозначать производную по времени точкой над переменной x предложил английский ученый сэр Исаак Ньютон (1642 — 1727). Обозначать производную штрихом f′(x) с 1797 года начал французский математик, астроном и механик Ж.Л. Лагранж (1736 — 1813). Частную производную ∂/∂x в своих работах независимо друг от друга ввели немецкие математики Карл Якоби (1805 — 1851) и Карл Вейерштрасс (1815 — 1897), но первенство такого обозначения, как свидетельствует хронология математических новшеств, принадлежит французскому математику А.М. Лежандру (1752 — 1833). Символ дифференциального оператора ∇ предложил выдающийся ирландский математик, механик и физик У.Р. Гамильтон (1805 — 1865) в 1853 году, а название «набла» - английский инженер, математик и физик Оливер Хевисайд (1850 — 1925) в 1892 году.
|

