Перезагрузка знаний » 2014 » Май » 21 » сущность сто
14:56:22

сущность сто

Преобразования Лоренца имеют вид


x'= Y(x- vt) (1)
t'= Y(t- vx/c2)                                        (2)
где: Y– безразмерный коэффициент

Y = Обратная величина квадратного корня                                            (3)

x и t – пространственная и временная координаты события в неподвижной системе К
x' и t' – аналогичные координаты в системе К', движущейся относительно системы К со скоростью v.

Пусть в системе К зафиксированы два пространственно-разобщенные  события (t1, x1) и м(t2, x2)[/b]. Перепишем (1) и (2):

x'2-x'1= Y[(x2-x1)- v(t2-t1)]                       (4)
t'2-t'1= Y[(t2-t1)- v(x2-x1)/c2]                   (5)

Введем понятие скорости протекания процесса u в неподвижной системе К:
u= (x2- x1 )/(t2-t1)                                    (6)

Тогда (4) и (5) примут вид:
x'2-x'1= (x2-x1)Y(1- v/u)                           (7)
t'2-t'1= (t2-t1)Y(1- vu/c2)                        (8)

Введем безразмерные величины:
p= (x'2-x'1 )/( x2-x1)                                  (9)
g= (t'2-t'1) /( t2-t1)                                  (10)

Получаем:
p= Y(1- v/u)                                             (11)
g= Y(1- vu/c2)                                           (12)

Как видно из (11) и (12),  при фиксированном значении v (Y=const), параметры p и g зависят только от скорости протекания процесса u в неподвижной системе К.

Используя  (11) и (12), построим графики зависимостей p=f(U) и g=f(U) (Рис 1 а) и б), скорость v – фиксированная)

Как видно из Рис. и (11), p=О при u=v. Кроме того, при u=±∞  p принимает значение p=Y (вырождается в аcимптоту). Казалось бы: постулат СТО запрещает все процессы, протекающие быстрее скорости света, но, тем не менее, в СТО и по сей день существует множество задачек и примеров,  в основе которых заложено u=±∞.

Совместим графики Рис 1 а) и б). Мы имеем право так поступить по тем причинам, что p и g - обе безразмерные и обе отражают один и тот же процесс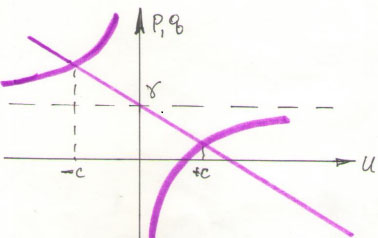

Пересечение кривых

Точки пересечения p и g получаем из условия p = g: 
u=±c.

Из аналитической геометрии следует, что кривые имеют общее решение только в точках пересечения.
Введем понятие скорости протекания процесса w в подвижной системе К':
w = (x'2-x'1 )/(t'2-t'1)                                 (13)
и разделим (7) на (8) с использованием (6). Получаем:
w = c2 u-v)/(c2-uv)                                   (14)

Итак, из преобразований Лоренца (1) и (2) мы получили формулу, связывающую четыре скорости:

1) u – скорость протекания процесса в неподвижной системе К;
2) w – скорость протекания процесса в подвижной системе К'
3) v – скорость движения подвижной системы К;
4) с – максимальная скорость протекания физического процесса в природе.

Формула (14) не зависит от Y, поэтому смело положим v =с, откуда следует w= -с, а u при этом может принимать абсолютно любые значения. Но это – очередной парадокс СТО, так как w по своей сути является отражением u. И только при u=с мы получаем w=c. 

Обратимся к параметрическому выводу преобразований Лоренца, а, именно, непосредственно к моменту определения функции  η , приводящей к вводу в уравнения Лоренца скорости света с.

Рассмотрим плоскую световую волну, распространяющуюся вдоль оси Х. В системе К уравнение волнового фронта имеет вид:

  x-ct=0                                                        (15)
а в подвижной системе К':
x'-ct'=0                                                       (16)

Так как в общем виде u = x/t
где: x2=x; x1=0; t2=t;  t1=0
то получается, что вместе с определением функции η мы определяем  u=с.

Проведя аналогичные действия с (16), получаем w=с.

Следовательно, СТО имеет право оперировать с процессами, происходящими в системах К и К' со скоростями u=w=с и ничего более. Когда рассматривается процесс, протекающий с другой скоростью, необходимо заново определять величину η и доказывать, что полученное значение η=c2 действительно имеет место в природе как конечное.

С учетом вышеизложенного,  (7) и (8) примут вид эффекта Доплера в релятивистской форме:
(x'2-x'1 )=(x2-x1)Корень квадратный                                       (17)
(t'2-t'1)=( t2-t1)Корень квадратный                                       (18)

Таким образом, преобразования Лоренца из двух пространственно-временных переплетенных уравнений превращаются в два независимых уравнения: чисто пространственное преобразование и чисто временное. Мат.анализ преобразований показывает, что СТО - это эффект Доплера в релятивистском виде. Но это - парадокс, поскольку скорость u=(x2- x1 )/(t2-t1 ) есть не что иное, как скорость движения самой подвижной системы v, что ведет к
парадоксальности СТО в целом.
Просмотров: 4345 | Добавил: vladimirphizik | Теги: СТО, электромагнитная теория гравитации, опровержение, специальная теория относительности | Рейтинг: 5.0/1

Метафизика – исследование общих черт структуры мира и наших методов проникновения в эту структуру.

- Макс Борн, один из создателей квантовой теории

Метафизика – это обыкновенная физика, только в руках ученого, который слишком далеко ходит за фактами.

- Сэмюэль Батлер

Есть только две поистине захватывающие темы, достойные серьёзных рассуждений: сплетни и метафизика.

- Иосиф Александрович Бродский

Метафизика – то, что над физикой
Словарь СЗЕФ: метафизика – это философское учение о граничных внеопытных принципах и началах бытия, знания и культуры
Джон Форбс Нэш-младший: Я верил в числа и термины, уравнения и логику, в здравый смысл... Но, проведя жизнь в подобных изысканиях, я не знаю, что такое логика, что определяет здравый смысл... Я прошел долгий путь через физику, метафизику, иллюзию... и обратно. И я сделал самое важное из своих открытий. Главное открытие моей жизни - логичные основания можно выявить только в таинственных уравнениях любви.
Перезагрузка