Анализ формулы с "золотым сечением" часть 1

Еще раз обратимся к формуле электромагнитной теории гравитации:



R = R₀{(√5 +1)/2}ⁿ ≈ R₀(1,6)ⁿ



где: n =0,1,2,3… - целочисленный показатель степени.

(√5 +1)/2 = 1,61803398875....≈ 1.6 - так называемое "золотое сечение"

R₀ - начальный параметр



Напомню некоторые примеры ее применения.



Первый пример

При R₀, равному радиусу Меркурия (R₀=2,4 тыс. км), получаем радиусы планет Солнечной системы:

1) n=0 R равен радиусу Меркурия 2,4 тыс. км

2) n=1 R=3.9 тыс. км.

Радиус Марса (табличное значение) равен 3,4 тыс. км.

3) n=2 R=6.2 тыс. км.

Радиус Венеры равен 6,1 тыс. км.

Радиус Земли равен 6,4 тыс. км

4) n=5 R=25,6 тыс. км

Радиус Нептуна равен 24,8 тыс. км.

Радиус Урана равен 26,2 тыс. км.

5) n=7 R=65,5 тыс. км

Радиус Сатурна равен 60,3 тыс. км

Радиус Юпитера равен 71,4 тыс. км.



Второй пример

Теперь в формулу подставляем 0.4а.е. (можем перейти в млн.км, что не принципиально) для Меркурия и проверяем

1) п=0 орбита Меркурия

2) п=1 получаем 0.6а.е. - Венера

3) п=2 - 1а.е - Земля

4) п=3 - 1.6а.е - Марс

5) п=4 - 2.6а.е. - астероиды (начало)

6) п=5 - 4.2а.е. - астероиды (конец)

7) п=6 - 6.7а.е. - Юпитер

8) п=7 - 10.7а.е. - Сатурн

9) п=8 - 17.1а.е. - Уран

10) п=9 - 27.4а.е. - Нептун

11)п=10 - 43.8а.е. - Плутон

(просто пример работы формулы).



Поищем, какую дополнительную информацию можно получить из этой формулы.



Рассчитаем отношение орбит планет (большая полуось, обозначим R) к радиусам непосредственно самих планет (обозначим r и используем общедоступные табличные данные).



Меркурий: 57.9млн.км/2.4тыс.км=24.1х10³

Везде будет коэффициент 10³, поэтому обойдемся без него.



Итак, расчеты:

Меркурий - 24.1

Венера - 17.7

Земля - 23.4

Марс - 67.0



Юпитер - 10.9

Сатурн - 23.7

Уран - 109.6

Нептун - 181.4



Теперь возведем число (1.6) в степень n, где n=0,1,2,3...

Получаем:

(1.6)⁵=10.5

(1.6)⁶=16.8

(1.6)⁷=26.84

(1.6)⁸=43.0

(1.6)⁹=68.7

(1.6)¹⁰=110.0

(1.6)¹¹=175.9



Уже видны совпадения рассчитанных величин.



Строим график: по оси Х - номер планеты, начиная с Меркурия N=1. Тогда у Венеры номер 2 и т.д. Но это не принципиально на данном этапе).

По оси Y откладываем отношения R/r без коэффициента 10 в третьей степени

:







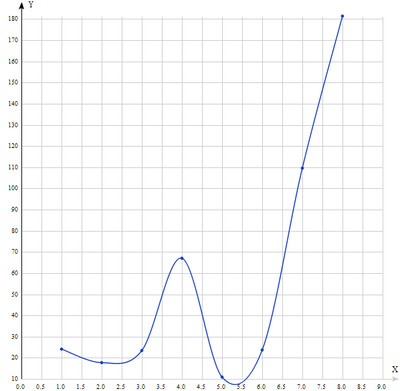
Теперь построим график, по оси X которого будем откладывать номер планеты (для Меркурия N=1 и далее), а по оси Y - разность между фактическими значениями отношений для планет от значений числа 1.6 в степени n. Получаем периодическую кривую:
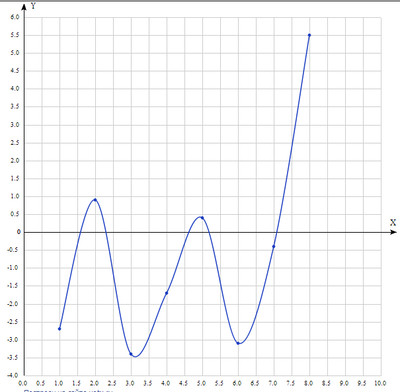