22:39:20 Длина дуги спирали | |
 в полярных координатах, то длина дуги l кривой выражается интегралом:  где  и  - значения полярного угла φ на концах вычисляемой дуги. Следовательно, длина дуги логарифмической спирали  границы которой заданы координатами  и  будет равна:  Из полученного выражения видно, что длина дуги логарифмической спирали пропорциональна приращению полярного радиуса дугиВсе это прекрасно, но в физике часто возникают ситуации, когда измерения необходимых величин затруднены теми или иными причинами. Например, каким образом можно измерить размеры полевого вихря атома, имеющего, к тому же, сложную динамичную структуру, да еще и в виде спирали? Для решения этой проблемы необходимо найти обходной вариант. И, как уже ранее сообщалось, таким вариантом является закон Бальмера-Ридберга (Структура поля). Казалось бы: при чем здесь закон Бальмера-Ридберга? Ответ очень прост: если внимательно посмотреть на серии излучений того же водорода, то отношение между первой линией и граничной трех серий лежит в пределах числа золотого сечения в первой степени 1.62, а трех других - в пределах числа золотого сечения 1.62 в третьей степени. 1) Серия Лаймана 91.15х1.62/121.6=1.214 2) Серия Бальмера 364.6х1.62/656.3=0.89997 3) Серия Пашена 820,4х1,62/1875,1=0,70878779798 4) Серия Брекетта 1458.0х1,62х1,62х1,62/4052.5=1,52960587884 5) Серия Пфунда 2279х1,62х1,62х1,62/7458=1,29917301046 6) Серия Хэмпфри 3281х1,62х1,62х1,62/12365=1,12812481747 Поскольку длина дуги золотой спирали 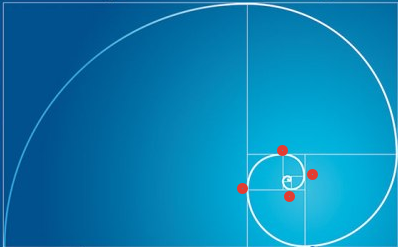 пропорциональна приращению полярного радиуса дуги, то получается, что серии Лаймана, Бальмера и Пашена формируются в первой и второй четверти витка золотой спирали, а серии Брекетта, Пфунда и Хэмпфри - в последней (четвертой) четверти золотой спирали. Но это - уже отдельная тема разговора. | |
|
| |
Метафизика – то, что над физикой
Словарь СЗЕФ: метафизика – это философское учение о граничных внеопытных принципах и началах бытия, знания и культуры
Джон Форбс Нэш-младший: Я верил в числа и термины, уравнения и логику, в здравый смысл... Но, проведя жизнь в подобных изысканиях, я не знаю, что такое логика, что определяет здравый смысл... Я прошел долгий путь через физику, метафизику, иллюзию... и обратно. И я сделал самое важное из своих открытий. Главное открытие моей жизни - логичные основания можно выявить только в таинственных уравнениях любви.
Перезагрузка
